Dijkstra寻路算法

有这样一个图：

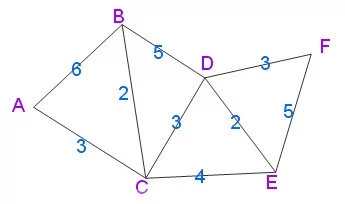
上图中，连线上的数字表示点与点之间的距离，那么从点A到点F的最短距离是多少？

重要

Dijkstra算法仅适用于所有点与点之间的距离都是非负的图。

为了解决这个问题，我们从出发点（点A）开始考虑，很显然，从A到A的最短距离是0。

接下来，从A到C直接走的距离是3，从A到B直接走的距离是6，而从A到C到B绕弯的距离是5，也就是说A到B点的最短距离我们没法直接判断，我们要试各种路径，找到最小值，才能知道它的最短距离。

也就是说，当A的最短距离为0刚刚确定下来的时候，与它相邻的点B和C的距离处于“暂未确定”状态，但是我们起码知道，如果采用直接走的方法他们的距离分别是B-6、C-3。

我们可以把所有的点分为三类：

• “已经确定”的点，我们把所有这类点的集合叫做“闭集”
• “暂未确定”的点，我们把所有这类点的集合叫做“开集”
• “还没开始计算”的点

此时，有一个很显而易见的道理，如果所有边的值都是非负的话，那么开集中最小距离那个点肯定已经确定了，例如上面那种情况，C的距离为3已经确定了。为什么呢？C的距离为3是最小的，其他的开集的点的值都比它大，因为所有边的值都是非负的，不管怎么绕路，距离都不会减少（一个较大的数+一个非负数，怎么都会越加越大）。

好了，开集中，一个点已经确定了，把他放入闭集中，与它相邻的“还没开始计算”的点可以算出直接走的距离，然后放入开集中。

接着，继续从开集中取距离最小的点，直到距离最小的点是目标点，或者开集为空为止。如果开集为空，说明没有路径可以到达目标点。

注意到，上面用下划线标注的那句话中，算与它相邻的点的情况可能有三种：

• 闭集的点，不用再回头算了；
• 开集的点，也许这样算出来的距离比之前算出来的距离短，那么说明这条更短，用它来替代暂时求出来的最短距离即可；
• “还没开始计算”的点。

这样一直重复算下去，当从开集中取出的点为F时，答案就出来了；或者当开集为空时，说明没有路径可以到达目标点。

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <tuple>

using namespace std;

const int INF = INT_MAX;

// 返回从start到end的最短距离，不可达返回-1
// 参数edges是一个集合，每个元素都是三元元组：(点1的序号, 点2的序号, 点1到点2的距离)
int dijkstra(int start, int end, const vector<tuple<int, int, int>>& edges, int nodeCount) {
    vector<int> dist(nodeCount, INF);
    // 使用最小堆优先队列，存储格式：(从起点到当前节点的距离, 当前节点的序号)
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;

    // 初始化起点
    dist[start] = 0;
    pq.emplace(0, start);

    while (!pq.empty()) {
        pair<int, int> top = pq.top();
        int current_dist = top.first;
        int u = top.second;
        pq.pop();

        if (u == end) return current_dist; // 找到目标点

        if (current_dist > dist[u]) continue;

        for (const auto& edge : edges) {
            int from = edge.first;
            int to = edge.second;
            int weight = edge.third;

            if (from != u) continue;

            if (dist[to] > dist[u] + weight) {
                dist[to] = dist[u] + weight;
                pq.emplace(dist[to], to);
            }
        }
    }

    return (dist[end] == INF) ? -1 : dist[end];
}